SEEING REFLECTIONS

Finding reflections in the real world is an interesting exercise.  They might not seem obvious right away, but once you start looking for them, you can find them in many places.  I'm going to find a type of reflection that's of interest to me, and offer three different ways to measure or quantify the reflection using mathematical terminology.

Where I looked for reflections?  The video game "PONG".  It was created in 1972, and is famous as one of the most basic video games.  It's a simple game, still entertaining to play today -- although it's not quite as exciting as current video game releases.  But it relies on the basic geometry of reflections, as you move your 'paddle' to bounce a ball back and forth.  Only by understanding reflections can you play the game effectively.

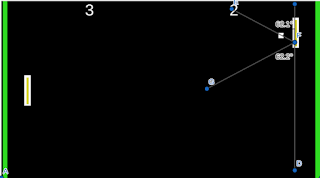
The first way to measure the reflections in Pong is using the angle.  In the screenshot below, you can see the ball approaching the paddle. The player needs to move the paddle to hit the ball; when that occurs, the ball will reflect off the paddle in the opposite direction.  To understand this reflection, we can look at the angle of the ball coming in and going out.  They are equal!   That is an important property of geometric reflections.

A second way to measure reflections in Pong is using slope.  In the figure below, we can see a ball in Pong bouncing off the bottom wall between the paddles.  Instead of measuring the angles of the lines, we can find the coordinates of the points on the ball's path, and calculate the slope of each line.
Using the slope formula, we find:
SLOPE of ED: (0-1.6)/(4-0) = -1.6/4 = -0.4
SLOPE of DC:  (2.6-0)/(10.3-4) = 2.6/6.3 = 0.41

Although it's off by a decimal of 0.01, we can see that the slopes of the two lines are about the same, but negative.  So we can see how reflected lines have NEGATIVE slopes.

The final way to look at reflections using Pong is by finding the actual equation of a line.  Looking at a final screenshot of the Pong game, we can detect two different lines representing the path of the ball as it reflects across the wall.  The reflection occurs at the point (7,8), so that means the ball is reflected across the line x = 7, which is indicated in the red dotted line.
Now, we can use the point-slope formula to find the equations of the two lines representing the ball.  
Slope CD = (4-8)/(10-7) = -4/3
Slope ED = (4-8)/(4-7) = -4/-3 = 4/3
The slopes are negative, like we noticed before!  Now, using the point-slope equation:
Line CD = y-8 = -4/3(x-7)  --> y = -4/3x + 52/3
Line ED = y-8 = 4/3(x-7)  ---> y = 4/3x + -4/3
You can see the lines have very different intercepts, but the slopes are related.

Having a line is useful since it allows me to predict where the ball will travel across the board.  Although when I'm playing the game I don't make these calculations, it does prove the value of understanding reflections and having effective ways to measure them, using mathematics.


Comments

Post a Comment

Popular posts from this blog

LENTILBALLS (TM)

For our food class this term we have beeen studying lots of interest and very important things. For instance, we did lots of baking. And we needed to learn some math and fractions becuase a lot of recipes have fractions. One thing that I enjoyed was seeing a farm in a restaurant. It didn't look like a farm, it looked someone's garden but really big. They called it a farm anyways so thats cool. We talked about leaveing agents emulsifers and protein. The major nutriitions are proteins, fats, and carbohydprates.   For our Action Project, we need to substitutie something in a recipe. Some people are substituting a emulsifeer. Some people re substituting a leaveing agent. I will do a substitution of meat with lentils instead.   for my experiment, I used the following meatball recipe: 1lb lean (at least 80%) ground beef 1/2cup Progresso™ Italian-style bread crumbs 1/4cup milk 1/2teaspoon salt 1/2teaspoon Worcestershire sauce 1/4teaspoon pepper 1small onion, finely chopped (
Read more

A WALK ON THE RIVER

Image
 Welcome to my introductory project that's introducing WATER and the SDG's!  We have had a buys week starting school, learning about the building and where we can eat lunch naerby, meeting all our friends, and larning LOTS of names.  In our classes we began to learn some things that are imporatnt for the class, like the SDGs.  That stands for Sustainable Development Goal, and it's imporatant for us because of the problems we have to learn about.  We also didn't learn some things, like our teacher won't tell us where he's from.  And I learned about Action Proejcts, where we create work instead of taking a test. For my very first action project, I am creating a poster.  My poster is trying to capture how cool it is that Chicago has a riverwalk.  For our FE we walked along the Riverwalk as a class, and observed how the peolpe use the river.  I saw a ton of boats.  The chairs were fun too.  I made a poster about the water, did you know that from 2015 to 2020, the pe
Read more